a) Đúng | b) Sai | c) Đúng | d) Sai
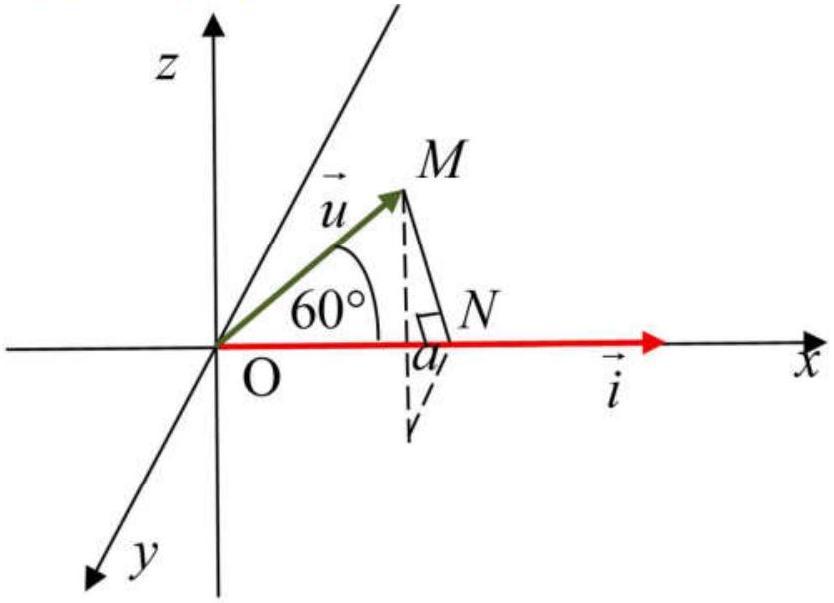
a) Vì góc giữa vectơ $\vec{u}$ với vectơ $\vec{i}$ là ${{60}^{\circ }}$. Nên ta có:
$\text{cos}{{60}^{\circ }}=\text{cos}\left( \vec{u},\vec{i} \right)=\dfrac{a.1+b.0+c.0}{\left| {\vec{u}} \right|}=\dfrac{a}{1}=a\Rightarrow a=\text{cos}{{60}^{\circ }}=\dfrac{1}{2}$.
Chọn ĐÚNG.
b) Ta có:
$\text{cos}{{60}^{\circ }}=\text{cos}\left( \vec{u},\vec{j} \right)=\dfrac{a.0+b.1+c.0}{\left| {\vec{u}} \right|}=\dfrac{b}{1}=b\Rightarrow b=\text{cos}{{60}^{\circ }}=\dfrac{1}{2}$;
$\text{cos}{{45}^{\circ }}=\text{cos}\left( \vec{u},\vec{k} \right)=\dfrac{a.0+b.0+c.1}{\left| {\vec{u}} \right|}=\dfrac{c}{1}=c\Rightarrow c=\text{cos}{{45}^{\circ }}=\dfrac{\sqrt{2}}{2};$
$\Rightarrow \vec{u}=\left( \dfrac{1}{2};\dfrac{1}{2};\dfrac{\sqrt{2}}{2} \right)$.
Theo giả thiết $\vec{u}$ là vectơ cùng hướng với vectơ $\overrightarrow{AB}$ nên $\vec{u}$ là VTCP của $AB$.
Vậy đường thẳng $AB$ có: $A\left( 5;5;0 \right)\in AB$ và có 1 VTCP $\vec{v}=2\vec{u}=\left( 1;1;\sqrt{2} \right)$.
Nên phương trình chính tắc của đường thẳng $AB$ là: $\dfrac{x-5}{1}=\dfrac{y-5}{1}=\dfrac{z}{\sqrt{2}}$.
Chọn SAI.
c) Ở thời điểm ban đầu $\left( t=0 \right)$, vật đi qua $A$ và hướng tới $B$. Sau 2 giây kể từ thời điểm ban đầu, vật đi được quãng đường 604 m. Ta có:
${{S}_{1}}=\int _{0}^{2}v\left( t \right)\text{dt}=\int _{0}^{2}\left( \beta t+300 \right)\text{dt}=\left. \left( \beta \dfrac{{{t}^{2}}}{2}+300t \right) \right|_{0}^{2}=604\Rightarrow \beta \dfrac{{{2}^{2}}}{2}+300.2=604\Rightarrow \beta =2$.
Chọn ĐÚNG.
d) Sau 5 giây kể từ thời điểm ban đầu, vật đến điểm $B$. Ta có:
$AB=S=\int _{0}^{5}v\left( t \right)\text{dt}=\int _{0}^{5}\left( 2t+300 \right)\text{dt}=\left. \left( {{t}^{2}}+300t \right) \right|_{0}^{5}={{5}^{2}}+300.5=1525$.
Theo giả thiết $\vec{u}$ là vectơ cùng hướng với vectơ $\overrightarrow{AB}$ nên:
$\overrightarrow{AB}=k\vec{u}\left( k{>}0,k=\dfrac{AB}{\left| {\vec{u}} \right|}=\dfrac{1525}{1}=1525 \right)$
$\Rightarrow {{x}_{B}}-{{x}_{A}}=k\cdot {{x}_{{\vec{u}}}}\Rightarrow {{x}_{B}}-5=1525\cdot \dfrac{1}{2}\Rightarrow {{x}_{B}}=767,5{<}768$.
Chọn SAI.
Phát biểu nào sau đây là đúng?
Đường thẳng $AB$ song song với mặt phẳng nào sau đây?
Đường tiệm cận đứng của đồ thị hàm số đã cho có phương trình là
Mật thư sẽ được giải nếu các bộ ba số xuất hiện ở những bộ ba vị trí $\left( A,M,B \right);\left( B,N,C \right)$; $\left( C,P,A \right)$ tạo thành các cấp số cộng theo thứ tự đó. Bạn Nam chọn ngẫu nhiên sáu số trong tập $S$ và xếp ngẫu nhiên vào các vị trí yêu cầu. Gọi xác suất để bạn Nam giải được mật thư ở lần chọn và xếp đó là $a$. Giá trị của $\dfrac{1}{a}$ bằng bao nhiêu?
Thể tích của khối chân đế bằng bao nhiêu centimet khối (không làm tròn kết quả các phép tính trung gian, chỉ làm tròn kết quả cuối cùng đến hàng phần mười).
